Biophotonic Instrumentation Group

Signal reconstruction using deep learning methods

May 2024 – Dec 2025

Master’s thesis

on the topic:

“Optical imaging through scattering media: Signal reconstruction using deep learning methods”

Katharina Seiffarth

“Seeing through” opaque or turbid barriers sounds like science fiction, yet optical research has pushed it closer to practice for decades. The core obstacle lies in strong multiple scattering. When light passes through media such as fog, milky glass, or biological tissue, photons scatter repeatedly and lose directional information. As a result, objects behind the medium disappear from direct view, and optical imaging depth in tissue drops sharply. This limitation constrains medical diagnostics and therapy, even though optical methods can offer high spatial resolution without ionizing radiation.

The work builds on a key insight: coherent laser illumination produces speckle, an interference pattern that looks random but still depends on the incoming wavefront and the microstructure of the scattering layer. Instead of treating speckle as noise, the thesis treats it as a measurable fingerprint that can encode information about the hidden object. If a model can learn the mapping from object to speckle, it may invert that mapping and recover the object.

Origin of speckle patterns. Coherent light hits a rough surface or scattering medium. The scattered waves travel different distances and interfere constructively or destructively, creating a characteristic granular pattern whose structure can be used by trained AI models to reconstruct hidden objects.

To test this idea, the thesis proposes and implements a laboratory optical setup that captures training pairs: known objects and their corresponding speckle patterns after the scattering layer. Deep neural networks then learn the relationship between object structure and speckle appearance. The experimental design uses a simplified lab scenario to isolate key factors, while still asking a practical question: can the trained model reconstruct previously unseen objects with useful fidelity?

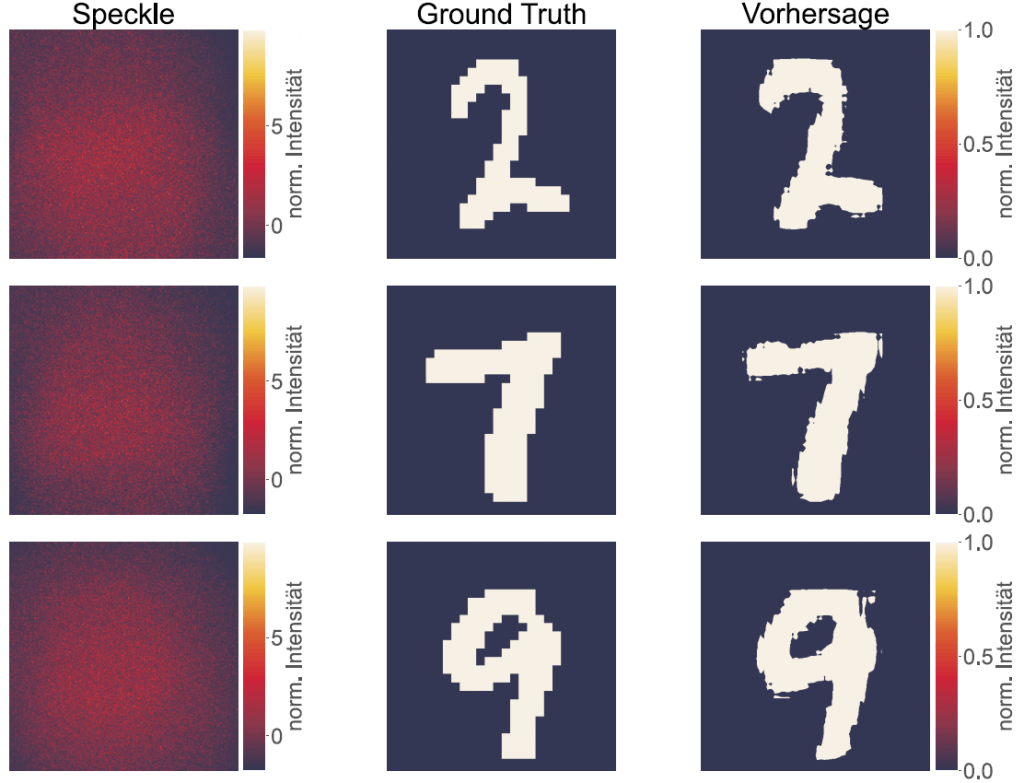
Deep learning reconstruction from speckle patterns. Input speckle (left), ground truth digit (center), and network prediction (right) for the example digits 2, 7, and 9.

A major motivation comes from current gaps in the field. Many published demonstrations focus on homogeneous targets (often digits or letters), struggle with dataset shifts, and frequently cap reconstruction sizes at 256×256 pixels. This thesis therefore aims for a dataset with higher variability and targets reconstructions of at least 512×512 pixels.

Methodologically, the work compares two loss functions and evaluates two network architectures. It also introduces a new loss term based on Laplace decomposition, designed to preserve fine detail. Finally, it explores transfer learning to reduce data requirements and potentially improve reconstruction quality.