AG Biophotonische Instrumentierung

Signalrekonstruktion unter Verwendung von Deep-Learning-Methoden

Mai 2024 - Dez. 2025

Masterarbeit

zum Thema:

"Optische Bildgebung durch streuende Medien: Signalrekonstruktion mittels Verfahren des Deep Learning"

Katharina Seiffarth

Das „Durchsehen“ undurchsichtiger oder trüber Barrieren klingt wie Science-Fiction, doch die optische Forschung hat dies seit Jahrzehnten näher an die Praxis herangeführt. Das zentrale Hindernis liegt in der starken Mehrfachstreuung. Wenn Licht durch Medien wie Nebel, Milchglas oder biologisches Gewebe hindurchgeht, streuen die Photonen wiederholt und verlieren ihre Richtungsinformation. Infolgedessen verschwinden Objekte hinter dem Medium aus dem direkten Blickfeld, und die optische Bildgebungstiefe im Gewebe nimmt stark ab. Diese Einschränkung behindert die medizinische Diagnostik und Therapie, obwohl optische Verfahren eine hohe räumliche Auflösung ohne ionisierende Strahlung bieten können.

Die Arbeit basiert auf einer wichtigen Erkenntnis: Kohärente Laserbelichtung erzeugt Speckle, ein Interferenzmuster, das zufällig aussieht, aber dennoch von der einfallenden Wellenfront und der Mikrostruktur der Streuschicht abhängt. Anstatt Speckle als Rauschen zu betrachten, behandelt die Arbeit es als messbaren Fingerabdruck, der Informationen über das verborgene Objekt kodieren kann. Wenn ein Modell die Zuordnung von Objekt zu Speckle lernen kann, kann es diese Zuordnung umkehren und das Objekt wiederherstellen.

Entstehung von Speckle-Mustern. Kohärentes Licht trifft auf eine raue Oberfläche oder ein streuendes Medium. Die gestreuten Wellen legen unterschiedliche Strecken zurück und interferieren konstruktiv oder destruktiv miteinander, wodurch ein charakteristisches körniges Muster entsteht, dessen Struktur von trainierten KI-Modellen zur Rekonstruktion versteckter Objekte genutzt werden kann.

Um diese Idee zu testen, schlägt die Arbeit einen optischen Laboraufbau vor und implementiert diesen, der Trainingspaare erfasst: bekannte Objekte und ihre entsprechenden Speckle-Muster nach der Streuschicht. Tiefe neuronale Netze lernen dann die Beziehung zwischen Objektstruktur und Speckle-Erscheinungsbild. Das Versuchsdesign nutzt ein vereinfachtes Laborszenario, um Schlüsselfaktoren zu isolieren, und stellt dennoch eine praktische Frage: Kann das trainierte Modell zuvor unbekannte Objekte mit brauchbarer Genauigkeit rekonstruieren?

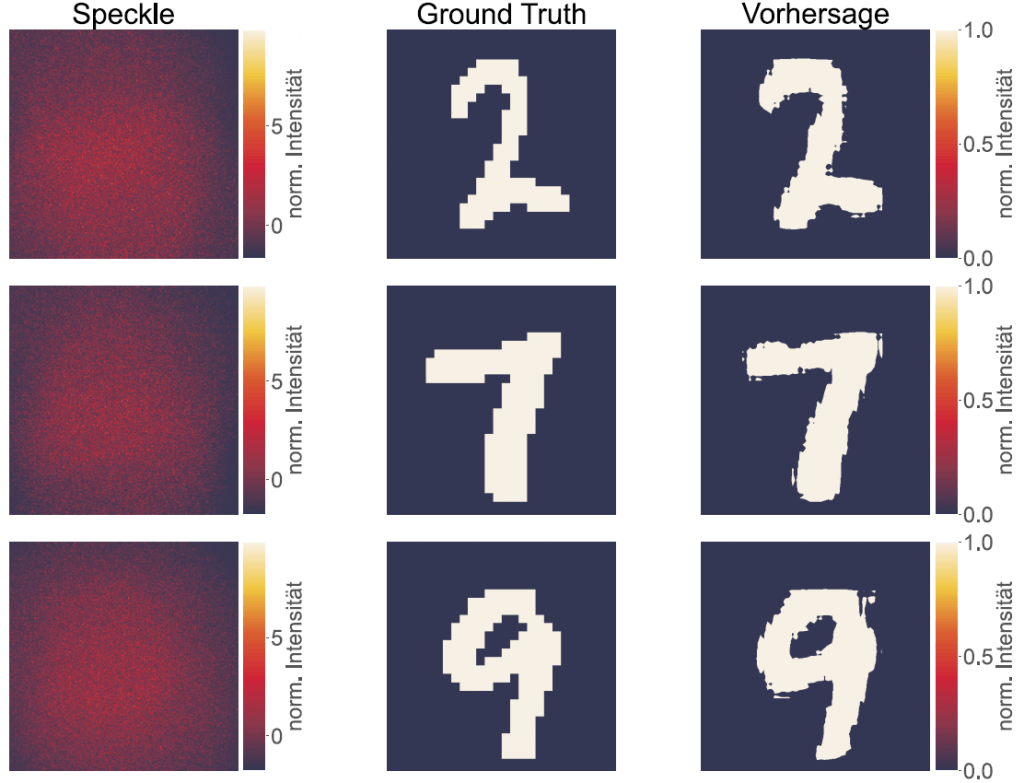
Deep learning reconstruction from speckle patterns. Input speckle (left), ground truth digit (center), and network prediction (right) for the example digits 2, 7, and 9.

Eine wichtige Motivation sind die derzeitigen Lücken in diesem Bereich. Viele veröffentlichte Demonstrationen konzentrieren sich auf homogene Ziele (oft Ziffern oder Buchstaben), haben Schwierigkeiten mit Datensatzverschiebungen und begrenzen die Rekonstruktionsgröße häufig auf 256×256 Pixel. Diese Arbeit zielt daher auf einen Datensatz mit höherer Variabilität und Rekonstruktionen von mindestens 512×512 Pixel ab.

Methodisch vergleicht die Arbeit zwei Verlustfunktionen und bewertet zwei Netzwerkarchitekturen. Außerdem wird ein neuer Verlustbegriff auf Basis der Laplace-Zerlegung eingeführt, der dazu dient, feine Details zu erhalten. Schließlich wird Transferlernen untersucht, um den Datenbedarf zu reduzieren und möglicherweise die Rekonstruktionsqualität zu verbessern.